I’ve gotten the lag time between posts down from 6 months to six weeks. Progress.
A topic that comes up often here is the effect of markups on aggregate productivity. And there is a recent-ish paper by David Baqaee and Emmanuel Fahri that has approached the relationship of markups (and distortions in general) with aggregate productivity from a very general perspective. By that I mean they show how to assess the impact of markups in an economy that may have some arbitrarily complex input-output structure for production, and in which it may be impossible to write down a coherent aggregate production function. In other words, they can assess the effect of markups on something approaching an actual economy.
My intention was to walk through some of their main theoretical results on how to track the effect of markups, and show you what they come up with when they use those results to quantify the effect of rising markups over time. And I’m going to get to that in a future post, which I promise will arrive in fewer than six weeks.
But in working on that post, I started to write up a short section to lay out how markups affect real GDP in the first place. This post is that section, and as you’ll see I failed completely on the “short” thing. It’s well over 2000 words and at some point involved a python program to draw the figure you’ll see below. So this review of the effect of markups is getting put up as its own post, and then I’ll use this to jump off into a more complete discussion of the BF results in the next one.
One of the key things that comes up in studying the role of markups is an apparent paradox. The presence of markups can mean the value of aggregate output is lower than it otherwise would be, as it leads to a misallocation of inputs. But at the same time, it is possible that raising the average markup in the economy will increase the value of aggregate output. It would appear as if markups can be both bad and good for output.
You’ll notice the hedges in those statements - “can mean” and “it is possible”. That is because these are not universal truths, but rather hold in specific circumstances. Once you understand how markups work in general, the circumstances under which this paradox arises will be more clear.
In explaining all this, I’m going to pursue exact opposite strategy of the BF paper, and show you how markups work in one very particular setup with only 2 goods and no interesting input-output structures between them. Keep in mind that BF establish how the intuition behind my simple example extends to more complex situations, and everything I’m doing here would still hold in general.
The bad effect of markups
Let’s say we’ve got an economy where there are two goods, 1 and 2. People want to consume both goods, but have diminishing marginal utility in consuming more of either one. Producers can make either good by using some input, and call it labor to be concrete. The technology to produce either good is simple. There is a constant marginal cost in terms of labor for producing one additional unit of a good, but that marginal cost might be different for the two goods. For example, if $MC_1 = 3$, then it takes 3 units of labor to produce one more unit of good 1. Note that if we flip this over, then $1/MC_1 = 1/3$ is additional output of good 1 we get from using 1 more unit of labor.
Having now dealt with preliminaries, what is the efficient outcome for this economy? And by efficient, I mean the outcome where the economy achieves the highest level of utility possible given the technology available and the stock of labor available. That outcome will be the point - the amount consumed of goods 1 and 2 - where the trade-off in utility between the two goods (the ratio of their marginal utilities) is exactly equal to the technological trade-off between the two goods (the ratio of their marginal costs). If you took intermediate economics, you might be familiar with this as the condition where the marginal rate of substitution equals the marginal rate of transformation,
\[\frac{MU_1}{MU_2} = \frac{MC_1}{MC_2}.\]I think it is helpful to rearrange this to see what is going on. So write
\[MU_1 \left(1/MC_1\right) = MU_2 \left(1/MC_2\right).\]On the left, this is the additional utility you would get if you put one more unit of labor to work producing good 1. You’d get, as mentioned, an additional $1/MC_1$ units of good 1 from that extra labor. Multiplying those units of good 1 by $MU_1$ tells us how valuable they are in terms of utility. If you did use one more unit of labor on good 1, though, you’d have to take that labor away from producing good 2. How much would you lose? You’d lose $1/MC_2$ units of good 2, and multiplying that by $MU_2$ would tell you how much utility you just sacrificed. When the utility gained from extra good 1 just equals the utility lost from less of good 2, then you haven’t improved your situation at all. And once we’re at the point where you can’t improve your situation at all, we’re at the efficient outcome.
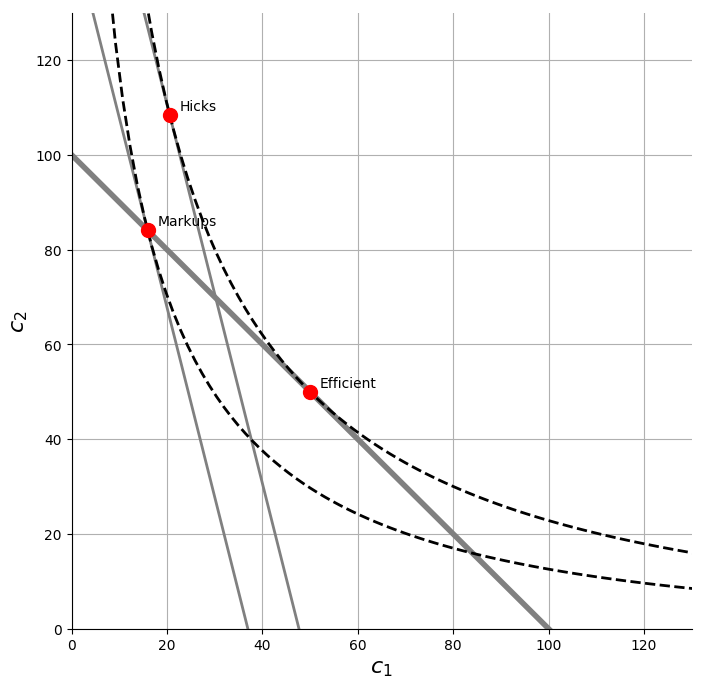
That was a lot of words. It is so much easier to see in a figure. What you can see labeled as the point “Efficient” is just the point at which the slope of the indifference curve (which is $-MU_1/MU_2$) is equal to the slope of the production possibilities frontier (which is $-MC_1/MC_2$). There is no feasible point we can produce (which is what the PPF captures) that gives us a higher level of utility.
Is it possible for the economy to reach that efficient outcome if no one is forcing it to reach that point? Sure, under some very specific conditions that boil down to the following
\[\frac{MU_1}{MU_2} = \frac{P_1}{P_2} = \frac{MC_1}{MC_2}.\]If we have that consumers take the prices of the goods as given, then they will buy goods until the ratio of their marginal utilities are equal to the ratio of prices. This is the point where their trade-off in utility is equal to the market trade-off between the two goods. On the other side, we need that for producers, the prices they charge are equal to the ratio of their marginal costs, or the technological trade-off is also equal to the market trade-off. In my figure, you can think of these conditions as saying that the budget constraint facing consumers (which tells consumers the ratio of $P_1$ to $P_2$) has the same slope as the PPF.
Now, what happens when firms are charging markups? By definition, a markup of price over marginal cost, $\mu_1$, means that the price charged is $P_1 = \mu_1 MC_1$ for good 1, with a similar expression for good 2. If there are markups, then we’ve got
\[\frac{MU_1}{MU_2} = \frac{P_1}{P_2} = \frac{\mu_1 MC_1}{\mu_2 MC_2}.\]In this case, you can see that even though consumers are doing their thing setting the ratio of marginal utilities equal to the ratio of prices, that ratio of prices is not necessarily equal to the ratio of marginal costs. And if the ratio of marginal utilities is not equal to the ratio of marginal costs, the economy cannot be at the efficient point.
If you look back at the figure, you an see what is happening. What I’ve done there is assume that there is a markup on good 1 relative to good 2. This means that the ratio of $P_1$ to $P_2$ is higher than the ratio of $MC_1$ to $MC_2$. For consumers, the budget constraint they face is steeper than the PPF, and so they naturally make the choice to consume less of good 1 and more of good 2. In the figure, I’ve shown the pure substitution effect of this change in prices with the point labeled “Hicks”. This holds their utility constant, but shows how choices shift when good 1 is pricier.
The problem with the “Hicks” point is that it is not feasible to produce. It lies outside of the PPF. We have to slide the budget constraint facing consumers backwards until their choices of what to consume given the marked up price for good 1 are possible to produce. That point is labeled “Markups”, and is where the economy ends up.
A few important notes on this “Markups” outcome. First, the economy is still on the PPF (the thick gray line). The problem with markups is not that they make the economy less technologically productive, or that they somehow push us inside the PPF (which would imply that we aren’t using all of our labor), but that they skew where along the PPF that we produce. Hence “misallocation” is the right way to characterize the effect of markups.
Second, it is not the existence of markups that creates a misallocation, it is dispersion in markups that creates a misallocation. To see this, go back to the last equation I showed. What would happen if both goods charged the same markup? Then $\mu_1 = \mu_2$, and we are back to $MU_1/MU_2 = MC_1/MC_2$. The economy would operate at the efficient outcome. Markups would imply that producer surplus had been increased at the expense of consumer surplus - there would be distributional consequences - but the economy would not be inefficient. Markups lower aggregate output when they differ across producers.
Third, note that I did not mention anything about why markups exist, or what kind of market power or market structure might allow them to exist. What the BF paper helped give me some clarity on was that, from the perspective of aggregate output, it is neither relevant nor necessary to know why markups exist, it is sufficient to know that they do.
A real quick aside here before I jump into the paradox of higher markups. I bounced back and forth a little above in talking about how markups lower the “value of output” or lower “utility”. Those are precise synonyms here. Measuring the value of output, as we try to do with real GDP, is measuring utility. We can argue about whether the BEA gets the calculations exactly right for the aggregate economy, but the principle still holds. So when I say that markups lower the value of output or utility in my little model here, that implies that measured real GDP would be lower as well.
Why higher average markups are associated with higher output
Given the situation I just described, how is it that higher average markups are associated with higher output? There are two ways this could work. To see the logic behind both, let me first define what I mean by average markup. This is the weighted average of the markups for the two goods, where the weights are their share in total spending. This would be something like $s_1 \mu_1 + s_2 \mu_2$, where $s_1$ is expenditures on good 1 relative to total expenditures.
(In practice, and to be consistent with BF, what we really want is the weighted harmonic mean of the markups. This is $(s_1/\mu_1 + s_2/\mu_2)^{-1}$. But while this is the technically accurate way of doing things, all the intuition you need to understand the paradox flows from the simple weighted average I started with.)
In the situation I set up in the figure, I said that the markup on good 1 was higher than on good 2, so $\mu_1 > \mu_2$, and that dispersion in markups lowered output. So we could raise output by raising the markup on good 2. If we got to the point where $\mu_2 = \mu_1$ again, then as I mentioned above, this would restore us to the efficient outcome. Raising $\mu_2$ up to the size of $\mu_1$ would obviously raise the average markup in the economy as well. Hence we have one example of the paradox of how higher average markups could be associated with higher output, even though “markups” (really, their dispersion) are associated with lower output.
A second possibility is that we leave the size of the markups themselves alone, but increase the expenditure share on good 1 with the high markup, $s_1$. This will raise the average markup in the economy, which should be obvious. But at the same time, this will act to raise total output, and hence give us the paradox again. How does this work? Remember, because of the fact that $\mu_1 > \mu_2$, it is the case that the $MU_1 (1/MC_1) > MU_2 (1/MC_2)$. In other words, we can gain utility by taking one unit of labor away from producing good 2 and switching it to producing good 1. In the figure above, the market didn’t make this move happen because as far as consumers are concerned the (marked up) prices of the goods are such that there is no gain to their utility from moving expenditure away from good 2 towards good 1. So anything that can induce a shift of expenditure away from 2 and towards 1 would raise the value of output.
What might induce such a change in expenditure? One thing would be if the productivity of producing good 1 increased, and hence $MC_1$ fell. This would make good 1 cheaper (the PPF and budget lines in the figure would become flatter), and people would buy more of good 1 than before, raising its expenditure share. The average markup would rise, and output would go up. You can see some of this logic by running the mental experiment out to an extreme. Let’s say that the marginal cost of producing good 1 fell towards zero, so that everyone consumed only good 1. Then we’re at a case where the economy is efficient - consumers want to consume only good 1, and the producers only make good 1 - but the average markup in the economy is exactly $\mu_1$. That situation might mean that producers are capturing most of the surplus, but as I said above, all we’re talking about here is the relationship of markups and the value of output, not its distribution.
If you are thinking through the possibilities, you’ll see that there is still a case where raising the average markup would lower the value of output. If the dispersion of markups gets worse, meaning that $\mu_1$ gets even higher, then the average markup would rise, and the economy would end up at a point with lower utility. You can see this if you think of making the budget line facing consumers in the figure steeper. Hence all the qualifications I made in the beginning of this post about the nature of the paradox of markups. There are circumstances in which higher average markups can hurt the economy, and circumstances in which it can help the economy (in terms of the value of output).
Technology, productivity and markups
The last thing I want to make clear is the distinction between productivity and technology, which I’ve been beating on for a while. Productivity is defined as the value of output divided by some measure of input use. Hence for my little toy economy, it is just utility divided by the units of labor used in production. Because the “Markups” point produces less utility than the “Efficient” point, but they use the same amount of labor, productivity in the “Markups” case is necessarily going to be lower.
Nevertheless, the technology in use at the “Markups” point is identical to the technology used at the “Efficient” point. The PPF did not move anywhere or change its slope because of the markups, and hence technology is the same at “Markups” and at “Efficient”.
If you think instead in terms of changes, or growth, then this intuition shows that productivity could grow (or not grow) for two reasons. First, technology could grow, meaning that the PPF shifts out, and then regardless of the markups we’d achieve higher utility. Second, the markups could change, and we could move along the current PPF, which would also change utility, and hence measured productivity. BF provide a way of breaking down changes in measured productivity into that contribution of the PPF itself versus the contribution of changes in markups, similar but not identical work by Basu and Fernald from 2002.
We’ll get to all of that - and more! - in the next post.